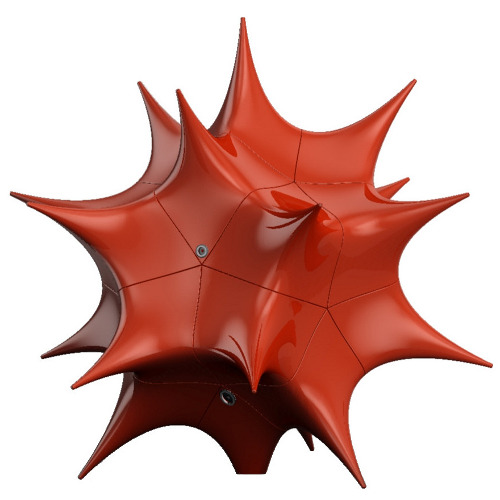
Dodecahedral Star
The sculpture "Dodekaederstern" was constructed on the occasion of the reopening of the former PVA-building at Rossauer Lände in Vienna for the Faculties of Mathematics and Economic Sciences in 2013. The geometric figure is defined in all of its details by just one algebraic equation. Its star shape refers to the name of the Oscar-Morgenstern-Platz and it illustrates the interplay of various fields of mathematics such as invariant theory, algebraic geometry, and singularity theory.
Mathematics
The surface of the sculpture is a real compact algebraic surface with isolated $A_2$-singularities in its $20$ cusps. Its symmetry group is the group $A_5\times \mathbb{Z}_2$ of the dodecahedron, whose elements permutate the vertices of the star. The $12$ intersection points of the $20$ parts lie on the centres of the dodecahedron's faces; so they describe the vertices of the icosahedron, which is the dodecahedron's dual platonic solid. The curvature of the star between its vertices is not uniquely determined and is regulated by the parameter $c$. The case $c=0$ describes the sphere; positive values yield outward-facing cusps while negative values yield vertices which are facing inwards (in such a case the resulting geometric figure is called an "anti-star").
Construction
The $20$ individual pieces of the sculpture are made of glass-fibre reinforced plastic (GRP). During construction the negative mould form is coated with a layer of gelcoat. The glass fabric and the glass mats as well as the core materials are then build up layer by layer and coated with resin. The parts are screwed together and sealed using flanges. The resulting GRP-structure is self-supporting. The finished structure is mounted on a steel frame using suspension cables.
Geometry and Algebra
The appeal of the dodecahedral star lies in the fact that it can be described by a single, albeit complicated, algebraic equation:
$$5c(2\varphi − 3)(x^2 − \varphi^2 y 2 ) (y^2 − \varphi^2z^2 )(z^2 − \varphi^2x^2 ) = (1 − (x^2 + y^2 + z^2 ))^3 − \frac{5}{27}c(x^2 + y^2 + z^2 )^3$$
with $\varphi=\frac{1+\sqrt{5}}{2}$ and free parameter $c$. The real solutions of this equation are triples of real numbers $(a,b,c)$, which, when substituted for $x$,$y$ and $z$, yield the same result on both left and right side of the equation. Not every such triple can be a solution, which is easily seen when substituting, for example, the values $(0,0,0)$ or $(1,2,3)$. On the contrary, only very special triples satisfy the equation and it is difficult finding or describing all such solutions.
Every triple $(a,b,c)$ of real numbers corresponds to a point in our space; for a given set of coordinates, this is just the point with $x$-coordinate equal to $a$, $y$-coordinate equal to $b$ and so on.
The mathematical theory tells us that the whole set of solutions of the above equation, meaning all triples taken together, forms a surface in the three-dimensional space. A priori it is very hard to determine its geometric shape from the defining equation. However, there exist visualization programs (for example POV-Ray) which can give an impression of the shape of such solution sets. In our case the solution set is the surface of the dodecahedral star. This is of course no coincidence; the equation was chosen exactly in such a way as to correspond to the geometric shape.
First we notice the symmetry of the star: five adjacent cusps form a regular pentagon and there are 12 such pentagons which all intersect at the same angle. This is the symmetry of the dodecahedron, one of the five platonic solids.
Furthermore we observe that the surface is smooth except for the $20$ cusps. These cusps are called singularities; they are of big importance to the study of the local geometry.
For the human brain it is rather easy to memorize the shape of the star; it is much harder to memorize the equation. However, using equations to describe geometric objects enables one to use algebraic methods, which, for example, can be used to compute visualizations or investigate further geometric properties.
The dialectic relation between algebra and geometry is one of the cornerstones of mathematics: here it appears in the example of the dodecahedral star. Finding the correct equation from the star's shape is not easy: this was done by Alexandra Fritz in her master's thesis using methods from invariant and singularity theory. There is some flexibility in altering the star's shape by changing the value of the free parameter $c$. The value $c=0$ yields the surface of the sphere; for increasing values of $c$ the cusps "grow" further out of the sphere. If $c$ is negative and decreasing, the sphere blows itself up and forms cusps which face inwards (see video).
The dodecahedral star is only one example of an algebraic surface with singularities and symmetries. The study of such surfaces is not yet finished and subject of extensive scientific work. At the Department of Mathematics at the University of Vienna there are several FWF ("Fonds Wissenschaftlicher Förderung") research grants supporting further work in this area.
The term "dodecahedral star" is sometimes used for another geometric figure, namely one of the Kepler-Poinsot polyhedra. The precise name of the latter is "stellated dodecahedron"; it is constructed by placing on each face of the dodecahedron a pyramid consisting of equilateral triangles. A representation of such a star can be found in a mosaic in the entrance hall of St Mark's Basilica in Venice; the mosaic is attributed to Paolo Ucello (Florence, 1397-1476).
The logo of the computer algebra system (CAS) "Mathematica" is similar in shape to the dodecahedral star; however, in the former the cusps are connected by lines whereas the latter is smooth everywhere outside of the cusps. So the symmetry is the same, but the local geometry is different. Additionally, the dodecahedral star can be described by a single equation.
Mathematical Foundations: A. Fritz & H. Hauser, Faculty of Mathematics, University of Vienna, FWF-Project P-21461.
Visualization: POV-Ray 3.6.
3-D Data Production : Institut Forwiss, Universität Passau, E. Fuchs, M. Kuhnkies, A. Zimmermann.
Data Adaption Nurbs: Fa. Evolute, A. Schiftner.
Mathematical Foundations
In order to construct the equation of the star from its geometric properties the following procedure was used: Let $G = A_5\times \mathbb{Z}_2 \subset O_3(\mathbb{R})$ denote the symmetry group of the dodecahedron. $G$ operates linearly on $\mathbb{R}^3$, which induces a natural group action on the polynomial ring $\mathbb{R}[x,y,z]$. The associated invariant ring $\mathbb{R}[x, y, z]^G$ of all $G$-invariant polynomials is a finitely generated $\mathbb{R}$-algebra if $G$ is a finite group - this is just the statement of the original version of Hilbert's finiteness theorem. In the case of a platonic solid the invariant ring is generated by three homogeneous polynomials. In our example the following two polynomials can be chosen as the generators:
$u = x^2 + y^2 + z^2$,
$v = (x^2 - \varphi^2 y^2) (y^2 - \varphi^2 z^2) (z^2 - \varphi^2 x^2)$,
where $\varphi=\frac{1+\sqrt{5}}{2}$ denotes the golden ratio. To ensure the symmetry of the star its equation is constructed as a polynomial $P(u,v)$ in the generator polynomials. The third generator has been ommited since, as it turns out, it is not needed. At this point both the coefficients and the degree of the polynomials are not known. It is also necessary to make sure that the symmetry group is finite (since then it would necessarily be isomorphic to $G$).
The next step is to prescribe the local geometry in the cusps of the star. It is sufficient to do this only for one of the cusps; the action of the group guarantees that the same will be true for the other cusps. The easiest singularity of the desired form is given by the equation $x^2 + y^2 = z^3$ - it is often referred to as the $A_2$-singularity. Now the taylor expansion of $P(u,v)$ as a polynomial in $x$,$y$, $z$ in one of the cusps is compared locally (and up to a diffeomorphism) to this equation. Results from deformation theory of singularities together with the specifications of the local geometry yield algebraic conditions for the coefficients of $P(u,v)$.
The resulting linear system of equations for the coefficients has, in general, no solutions if the degree of $P$ is chosen to be small. For the dodecahedral star the first degree for which real solutions appear is $d=3$. These solutions are not unique but form a $1$-dimensional family, parametrized by the real value $c$. One obtains the following equation for the star:
$f = 5c(2\varphi − 3)v - (1 − u)^3 + \frac{5}{27} cu^3 = 0$
If $c=0$ then the equation describes just the $2$-sphere. Therefore let $c\neq0$. One has to prove that, besides the cusps, there are no other singular real points on the surface. This finally yields the equation. The exact form of the star for a chosen value c can be visualized using computer programs. One observes that changing the parameter c affects the curvature between the cusps. For the sculpture the value $c=81$ has been chosen.
For more detail on the mathematical background see the article of Alexandra Fritz and Herwig Hauser.
Technical Details
Star-shaped sculpture made out of GRP:
- Fiberglass composite (GRP)
- 20 individual segments "Fünfeckknoten"
- GRP-assembly self-supporting
- Thickness (walls) 7mm
- Master-form milled, including negative molds for production
- "Sandwich"-structure as a mixed laminate
- Individual segments bolted and sealed by flanges
- Outer surface Gelcoat RAL 3003
- Total weight of GRP structure: 400kg
Outer coating: Gelcoat Ral 3003, applied to negative forms before lamination, Fa. Steiner, Fa. Wildschek.
Inner frames: Stahl, Stahlundform, P. Fraiss.
Suspension:
- Suspension using 6 steel cables PE7 ø10 mm, preload below: 2.2 t, preload top: 1.4 t.
- Connection via steel inner frame with 2x3-way connection of the traction cables
- Masts made of round steel ø200 mm, wall thickness 25 mm, height 5400mm, outside slope before preload: 258 mm
Foundation: Triangular base plate made out of reinforced concrete, length: 8m, thickness: 0.4m. Fa. Edom Bau.
Static of the sculpture & suspension: DI C. Petz.
Permit application: Arge GP.
Lighting: 3 headlights Bega 7704 Led 30,0W + 796, O. Kressl, Fa. Csernohorszky.
Contracting and construction management: University of Vienna, Vizerektorat für Infrastruktur, Abteilung für Raum und Ressourcenmanagement, Fa. Alltech
Funding: Universität Wien, Raiffeisen-Holding NÖ-Wien, FWF Projekt P21461
Idea, concept & design: H. Hauser, Faculty of Mathematics, University of Vienna.











