Legende
Die Skulptur "Dodekaederstern" wurde anlässlich der Adaptierung des ehemaligen PVA-Gebäudes an der Rossauer Lände für die Fakultäten der Mathematik, bzw. der Wirtschaftswissenschaften der Universität Wien im Jahr 2013 realisiert. Idee und Entwurf stammen von Herwig Hauser von der Fakultät für Mathematik. Die Figur wird durch eine einzige mathematische Gleichung in jedem Detail bestimmt. Die Sternform nimmt Bezug auf die Namensgebung des Oskar-Morgenstern-Platzes und illustriert das Zusammenspiel der mathematischen Gebiete Invariantentheorie, Algebraische Geometrie und Singularitätentheorie.
Mathematik
Die Oberfläche der Skulptur ist eine reelle, kompakte algebraische Fläche mit isolierten $A_2$ -Singularitäten in den zwanzig Spitzen. Ihre Symmetriegruppe ist die Gruppe $A_5$ des Dodekaeders, deren Elemente die Spitzen permutieren. Die 12 Begegnungspunkte der 20 Einzelteile liegen an den Flächenmittelpunkten des Dodekaeders, beschreiben also die Ecken des dualen Ikosaeders. Die Krümmung des Sterns zwischen den Spitzen ist nicht eindeutig festgelegt und wird durch einen Parameter $c$ reguliert. Der Wert $c = 0$ entspricht der Sphäre, positive Werte liefern nach aussen gerichtete Spitzen, negative nach innen zeigende Spitzen (Anti-Stern).
Herstellung
Die zwanzig Einzelteile der Sternskulptur bestehen aus Glasfaserverbundwerkstoff GFK. Die Negativform wird bei der Herstellung mit Gelcoat beschichtet. Glasgewebe und Glasmatten, sowie das Kernmaterial werden anschließend lagenweise aufgebaut und mit Harz imprägniert. Die Segmente werden zueinander über Flansche verschraubt und abgedichtet. Die GFK-Struktur ist selbsttragend. Die Aufhängung erfolgt durch Anbindung der Zugseile an ein innenliegendes Stahlgerüst.
Geometrie und Gleichung
Der Reiz der Figur ist die Tatsache, dass sie durch eine einzige, wenn auch komplizierte, algebraische Gleichung definiert werden kann, nämlich durch
$$5c(2\varphi − 3)(x^2 − \varphi^2 y 2 ) (y^2 − \varphi^2z^2 )(z^2 − \varphi^2x^2 ) = (1 − (x^2 + y^2 + z^2 ))^3 − \frac{5}{27}c(x^2 + y^2 + z^2 )^3$$
mit $\varphi=\frac{1+\sqrt{5}}{2}$ und freiem Parameter $c$. Die reellen Lösungen dieser Gleichung sind Tripel von Zahlen $(a, b, c) \in \mathbb{R}^3$ , die beim Einsetzen in die Gleichung für $x$, $y$ und $z$ auf linker und rechter Seite das gleiche Resultat liefern. Nicht jedes Tripel kann Lösung sein, wie man sich leicht am Beispiel $(0, 0, 0)$ oder $(1, 2, 3)$ durch Nachrechnen überzeugt. Im Gegenteil, nur sehr spezielle Tripel erfüllen die Gleichung, und es ist schwierig, alle Lösungen zu finden oder zu beschreiben.
Jedes Zahlentripel $(a, b, c)$ entspricht einem Punkt in unserem Raum: für ein gegebenes Koordinatensystem ist dies gerade der Punkt mit $x$-Koordinate $a$ (Abstand nach links vom Ursprung), $y$-Koordinate $b$ (Abstand nach vorne vom Ursprung) und $z$-Koordinate $c$ (Abstand nach unten vom Ursprung).
Die mathematische Theorie sagt uns nun, dass die gesamte Lösungsmenge der obigen Gleichung, das heisst, alle Lösungstripel zusammen genommen, eine Fläche im dreidimensionalen Raum bildet. A priori ist es sehr schwer, die geometrische Form dieser Fläche aus der Gleichung zu erkennen. Allerdings gibt es Visualisierungsprogramme wie etwa POV-Ray, die dies schon sehr gut bewerkstelligen und uns einen Eindruck von der Gestalt vermitteln können. Im gegenständlichen Fall ist die Lösungsmenge der Gleichung die Oberfläche des Sterns. Das ist kein Zufall, die Gleichung wurde genauso gewählt.
Wir beobachten als erstes die Symmetrie der Figur: jeweils fünf Spitzen bilden ein regelmässiges Fünfeck, und es gibt 12 solcher Fünfecke, die jeweils mit den gleichen Winkeln aneinanderstossen. Dies ist die Symmetrie des Dodekaeders, einer der fünf platonischen Körper.
Weiters stellen wir fest, dass die Fläche glatt ist mit Ausnahme der 20 Spitzen. Diese Punkte heissen Singularitäten; sie sind besonders aufschlussreich für das Studium der lokalen Geometrie.
Das menschliche Gehirn kann mit wenig Aufwand die Gestalt der Skulptur abspeichern und memorieren. Hingegen ist es fast unmöglich, sich die Gleichung zu merken. Diese hat aber den Vorteil, dass sie sich algebraischen Methoden unterziehen lässt. Damit wird beispielsweise die Visualisierung produziert, oder das genauere Studium der Geometrie durchgeführt. Die Dialektik Geometrie–Algebra ist ein Grundpfeiler der Mathematik: sie manifestiert sich am Beispiel des Sterns, wobei es nicht einfach ist, aus der Kennntis der Form die richtige Gleichung (sie ist im Wesentlichen eindeutig) zu finden: Dies wurde von Alexandra Fritz in ihrer Masterarbeit mit Hilfe von Invarianten- und Singularitätentheorie erfolgreich bewerkstelligt. Eine gewisse Flexibilität ergibt sich aus der Wahl eines freien Parameters $c$, der bei der Skulptur mit dem Wert $c = 81$ belegt wurde. Er bestimmt, wie spitz der Stern ist. Der Wert $c = 0$ liefert die Kugeloberfläche, und bei wachsendem $c$ wachsen die Spitzen zusehends aus der Kugel heraus. Wird $c$ kleiner, also negativ, so bläst sich die Kugel auf und bildet dabei nach innen zeigende Spitzen.
Der Dodekaederstern ist nur ein Beispiel einer algebraischen Fläche mit Singularitäten und Symmetrien. Ihr Studium ist bei weitem noch nicht abgeschlossen und Gegenstand intensiver Forschungsarbeiten. An der Fakultät für Mathematik der Universität Wien wird es durch mehrere Forschungsprojekte des FWF (Fonds Wissenschaftlicher Förderung) besonders unterstützt.Der Name "Dodekaederstern" wird gelegentlich für eine andere Figur verwendet, nämlich einen der Kepler'schen Sternkörper. Die englische Bezeichnung "stellated dodecahedron" präzisiert die Konstruktion: Man setzt auf jede (fünfeckige) Seitenfläche des Dodekaeders eine Pyramide aus gleichseitigen Dreiecken. Ein Mosaik dieses Sterns findet sich im Eingangsbereichs des Markusdoms in Venedig. Es wird Paolo Ucello (Florenz 1397 - 1475) zugeordnet.
Das Logo des Computeralgebra Programms "Mathematica" ähnelt in seiner Form dem Dodekaederstern, unterscheidet sich aber insoweit, als dass die Spitzen durch Grate verbunden sind, während beim Stern die Oberfläche ausserhalb der Spitzen überall glatt ist. Die Symmetrien stimmen also überein, nicht hingegen die lokale Geometrie. Zudem wird der Stern durch eine einzige Gleichung beschrieben.
Mathematische Grundlagen: A. Fritz & H. Hauser, Fakultät für Mathematik, Universität Wien, im Rahmen des FWF-Projektes P-21461.
Visualisierung: POV-Ray 3.6.
Produktion 3-D Daten: Institut Forwiss, Universität Passau, E. Fuchs, M. Kuhnkies, A. Zimmermann.
Datenadaptierung Nurbs: Fa. Evolute, A. Schiftner.
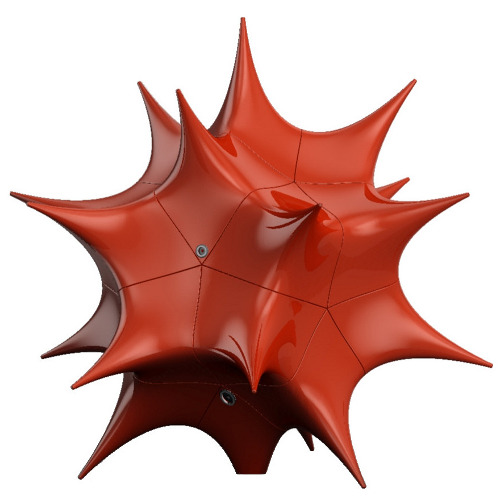
Mathematische Grundlagen
Zur Konstruktion der Gleichung aus der geometrischen Vorgabe wurde folgendes Verfahren verwendet. Es bezeichne $G = A_5\times \mathbb{Z}_2 \subset O_3(\mathbb{R})$ die Symmetriegruppe des Dodekaeders. Sie operiert linear auf $\mathbb{R}^3$ , wodurch eine natürliche Operation auf dem Polynomring $\mathbb{R}[x, y, z]$ induziert wird. Der zugehörige Invariantenring $\mathbb{R}[x, y, z]^G$ aller $G$-invarianten Polynome ist nach Hilbert für jede endliche Gruppe eine endlich erzeugte $\mathbb{R}$-Algebra. Sie wird bei platonischen Körpern von drei homogenen Polynomen erzeugt. In unserem Beispiel können für die ersten zwei Erzeuger des Invariantenringes etwa die Polynome
$u = x^2 + y^2 + z^2$,
$v = (x^2 - \varphi^2 y^2) (y^2 - \varphi^2 z^2) (z^2 - \varphi^2 x^2)$
gewählt werden, wobei $\varphi=\frac{1+\sqrt{5}}{2}$ den goldenen Schnitt bezeichnet (der dritte Erzeuger ist komplizierter). Die Symmetrie des Sterns wird nun sichergestellt, indem man die Gleichung der Fläche durch ein Polynom $P(u, v)$ in den invarianten Polynomen definiert. Es stellt sich heraus, dass der dritte Erzeuger nicht benötigt wird. Der Grad dieses Polynoms ist noch offen, ebenso wie seine Koeffizienten. Zudem ist sicherzustellen, dass die Symmetriegruppe endlich ist (dann ist sie notwendig gleich $A_5\times \mathbb{Z}_2$ ).
Als nächstes wird die lokale Geometrie in den Spitzen des Sterns vorgeschrieben. Es genügt, sie in einer Spitze festzulegen, durch die Operation der Gruppe setzt sie sich in alle anderen Spitzen fort. Die einfachste Singularität der gewünschten Gestalt ist durch die Gleichung $x^2 + y^2 = z^3$ gegeben, die sogenannte $A_2$ - Singularität. Die Taylorentwicklung von $P(u, v)$ als Polynom in $x$, $y$, $z$ in einem einer Spitze entsprechenden Punkt wird nun lokal und bis auf Diffeomorphie mit dieser Gleichung verglichen. Die Vorgabe der lokalen Geometrie impliziert via der Deformationstheorie von Singularitäten algebraische Bedingungen an die Koeffizienten von $P(u, v)$.
Das resultierende Gleichungssystem für die noch unbekannten Koeffizienten hat für kleinen Grad von $P$ im Allgemeinen keine Lösung. Für den Dodekaederstern ist $d = 3$ der erste Grad, bei dem reelle Lösungen auftreten. Diese sind nicht eindeutig, sondern bilden eine eindimensionale Schar, parametrisiert durch einen reellen Wert $c$. Man erhält für den Stern die Gleichung
$f = 5c(2\varphi − 3)v - (1 − u)^3 + \frac{5}{27} cu^3 = 0$
Der (uninteressante) Wert $c = 0$ liefert die $2$-Sphäre. Sei also $c \neq 0$. Es ist nun nachzurechnen, dass außer in den Spitzen keine weiteren (reellen) singulären Punkte vorliegen können. Damit ist die Gleichung gefunden. Die exakte Form des Sterns für jedes c bestimmt man am besten durch ein Visualisierungsprogramm. Man stellt fest, dass der Wert c die Krümmung des Sterns zwischen den Spitzen beeinflusst. Für die Skulptur wurde $c = 81$ gewählt.
Die detaillierte Beschreibung der zugrunde liegenden mathematischen Überlegungen finden sich in der Arbeit von A. Fritz und H. Hauser.
Technische Details
Sternskulptur aus GFK:
- Glasfaserverbundwerkstoff (GFK)
- 20 Einzelsegmente "Fünfeckknoten"
- GFK-Baugruppe selbsttragend
- Wandstärke 7mm
- Urmodell gefräst, davon Negativformen für Produktion
- Sandwichaufbau als Mischlaminat
- Segmente zueinander über Flansche verschraubt und abgedichtet
- Aussenflächen Gelcoat RAL 3003
- Gesamtgewicht GFK 400kg
Oberschicht: Gelcoat Ral 3003, auf Negativformen vor Laminierung aufgetragen, Fa. Steiner, Fa. Wildschek.
Innengerüst: Stahl, Stahlundform, P. Fraiss.
Aufhängung:
- Aufhängung über 6 Stahlseile PE7 ø10mm, Vorspannung unten 2,2t, oben 1,4t
- Anbindung über Stahlinnengerüst mit 2x3-fach Anbindung der Zugseile
- Masten aus Rundstahl ø200 mm, Wandung 25 mm, Höhe 5400mm, Aussenneigung vor Vorspannung 258 mm
Fundament: Dreieckige Bodenplatte Stahlbeton, 8m Seitenlänge, 0,4m Dicke. Fa. Edom Bau.
Statik Stern & Aufhängung: DI C. Petz.
Einreichplanung: Arge GP.
Beleuchtung: 3 Scheinwerfer Bega 7704 Led 30,0W + 796, O. Kressl, Fa. Csernohorszky.
Auftraggeber und Bauleitung: Universität Wien, Vizerektorat für Infrastruktur, Abteilung für Raum und Ressourcenmanagement, Fa. Alltech
Finanzierung: Universität Wien, Raiffeisen-Holding NÖ-Wien, FWF Projekt P21461
Idee, Konzept, Gestaltung: H. Hauser, Fakultät für Mathematik, Universität Wien.











